Community detection on geometric graphs
A local-to-global perspective
B. R. Vinay Kumar
NETWORKS Training week
April 9, 2025
Kaap Doorn, Netherlands
Geometric graphs
Wireless networks
Social networks
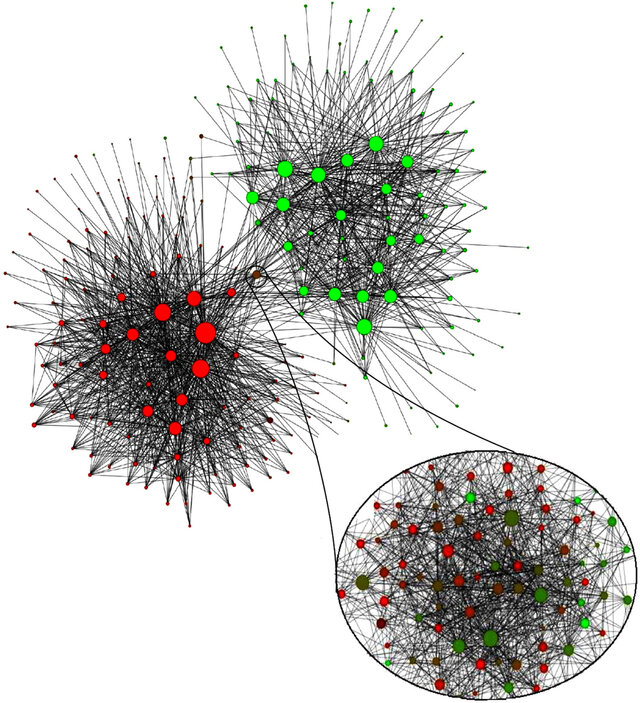
Data science
- Geometric graphs? Vertices are embedded in a metric space and edges depend on the distance between nodes.
- Presence of short edges and abundance of triangles.
Questions?
- How does the network structure affect processes or information on the network?
- Can local algorithms help to solve a global problem?
- Does geometry help in solving a global problem efficiently?
Community detection
Partition the vertex set of a graph into subsets meaningfully.
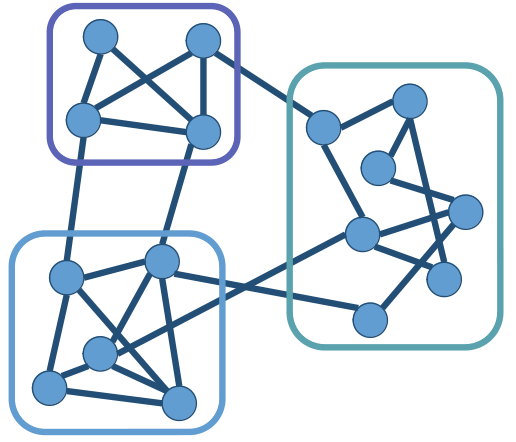
Group of nodes that are more connected to one another than to the rest of the network.
Two approaches
- Model-based methods: Build a model from data and design algorithms for the model.
- Model-free methods: Modularity based methods, Louvain algorithm etc.
Community detection
Co-authorship networks
Community detection

Interactions depend on:
- Node communities
- Distance between nodes
- Vertex weights
Co-authorship networks
Model
Torus \( S=\left[\frac{-1}{2},\frac{1}{2}\right]^d\)
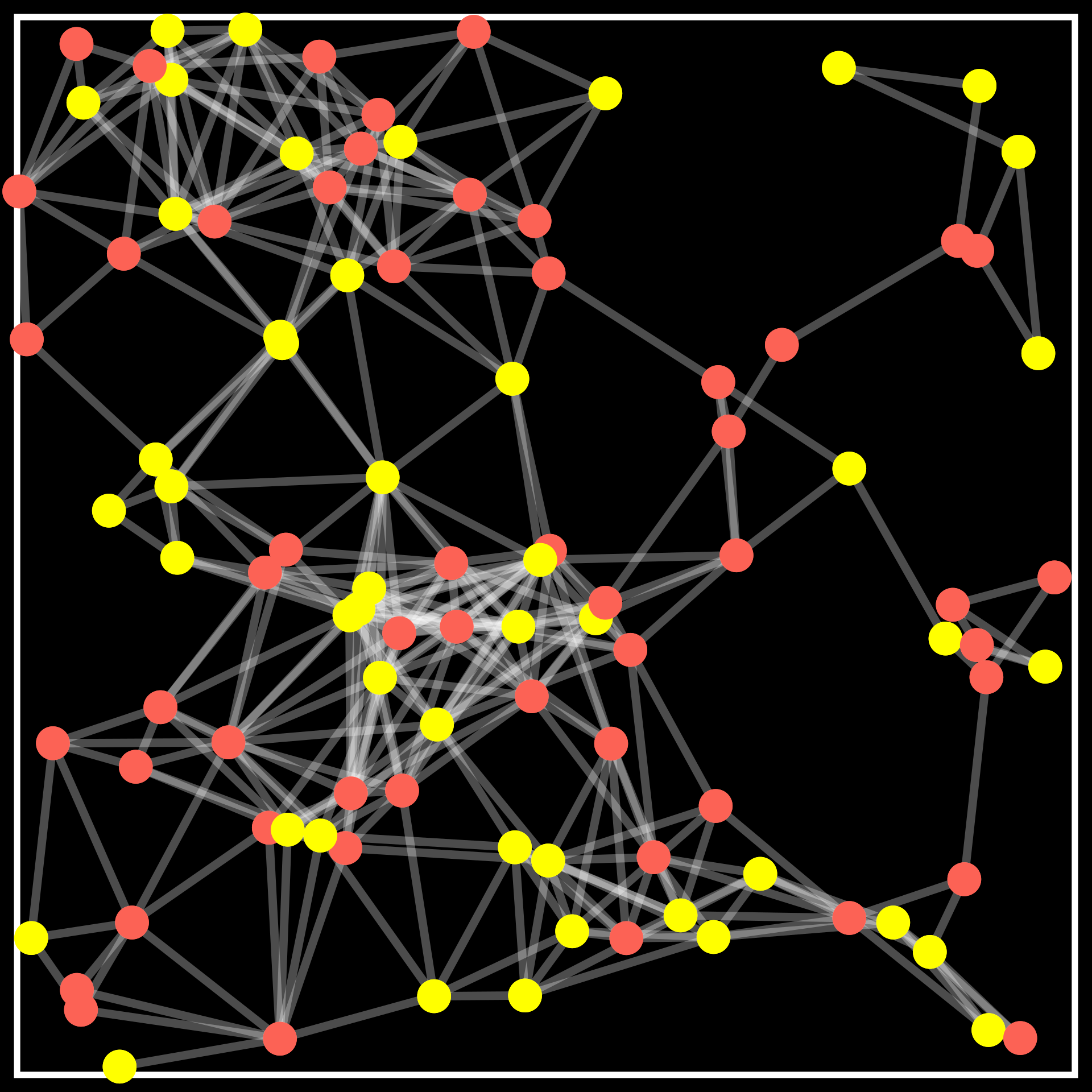
\(\mathbf{A}\) \(\sim GKBM(\lambda,n,d,\kappa_{\text{in}},\kappa_{\text{out}})\)
- Poisson point process \(\mathbb{X}\)\(= \{X_u\}_{u=1}^N\) of intensity \(\lambda n\)
- Sample $N \sim \text{Poi}(\lambda n)$.
- Choose \(X_1,X_2,\cdots,X_N\) uniformly from $S$.
- Weights: \(\mathbf{W}\)=\(\big(W_1,W_2,\cdots, W_N\big), \ \ W_i\in \mathcal{W} \sim F_W(\cdot)\)
- Two communities: \( \sigma\)\( = \big(\sigma(1),\cdots,\sigma(N)\big)\) \[\mathbf{P}(\sigma(u)=\color{#f86d6d}{+1})=\mathbf{P}(\sigma(u)=\color{#ffde20}{-1}) = \frac{1}{2}\]
- Geometric kernels: \(\kappa_{\text{in}},\kappa_{\text{out}}: \mathbb{R}^+\times\mathcal{W}\times \mathcal{W}\to [0,1]\)
- \(\alpha_{n,d} = \big(n/\log n\big)^{1/d}\)
Given locations \(\mathbb{X}\), weights \(\mathbf{W}\) and communities \(\sigma\)
\[A_{uv}=1 \text{ w.p. }\begin{cases} \kappa_{\text{in}}\big(\alpha_{n,d}\|X_u-X_v\|,W_u,W_v\big) & \text{if } \sigma(u)=\sigma(v)\\ \kappa_{\text{out}}\big(\alpha_{n,d}\|X_u-X_v\|,W_u,W_v\big) & \text{if } \sigma(u) \neq \sigma(v) \end{cases}\]
Problem Formulation
\(\mathbf{A}\) \(\sim GKBM(\lambda,n,d,\kappa_{\text{in}},\kappa_{\text{out}})\)
Problem: Given the locations \(\mathbb{X}\), the weights \(\mathbf{W}\) and the graph \(\mathbf{A}\), recover \( \sigma_n\) exactly.

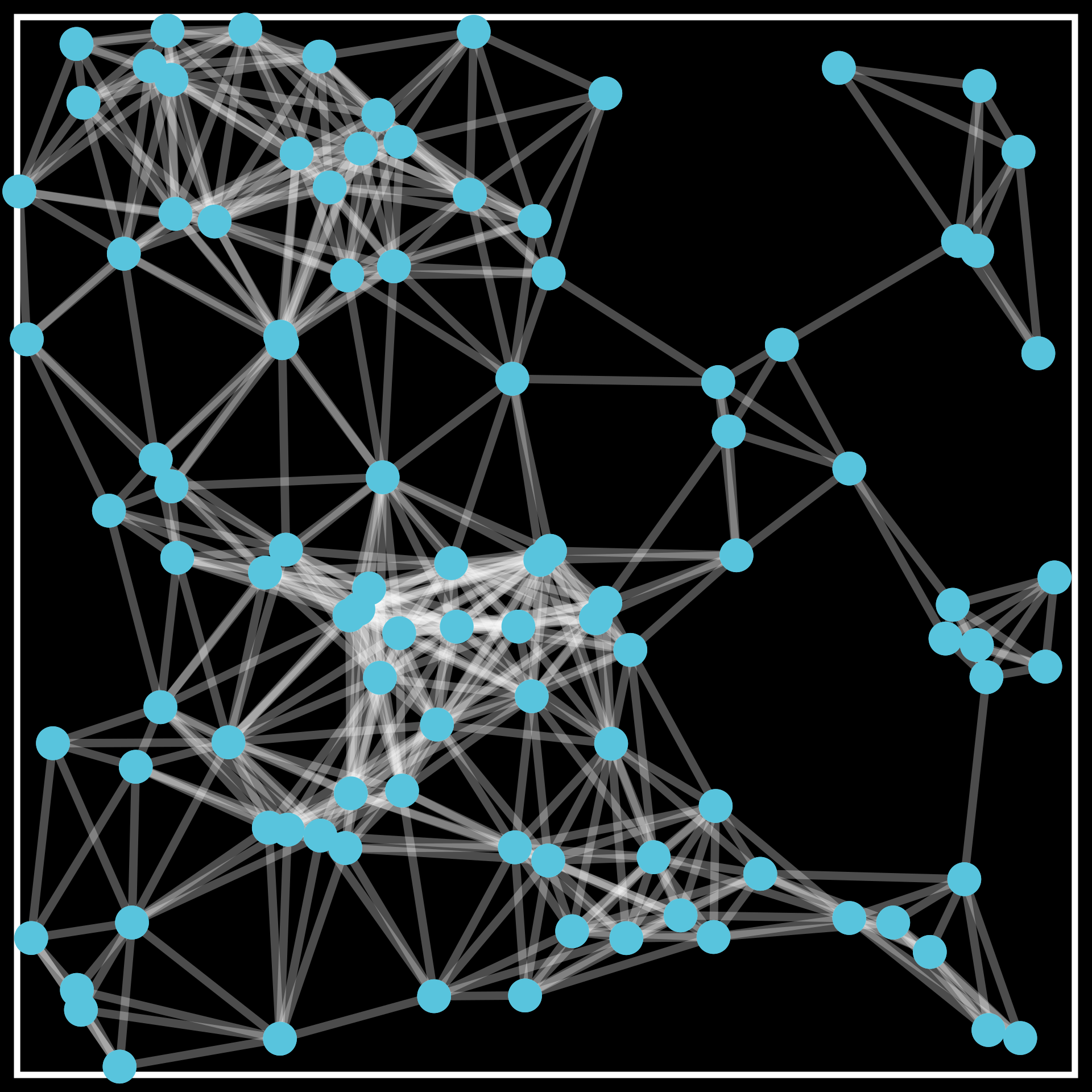

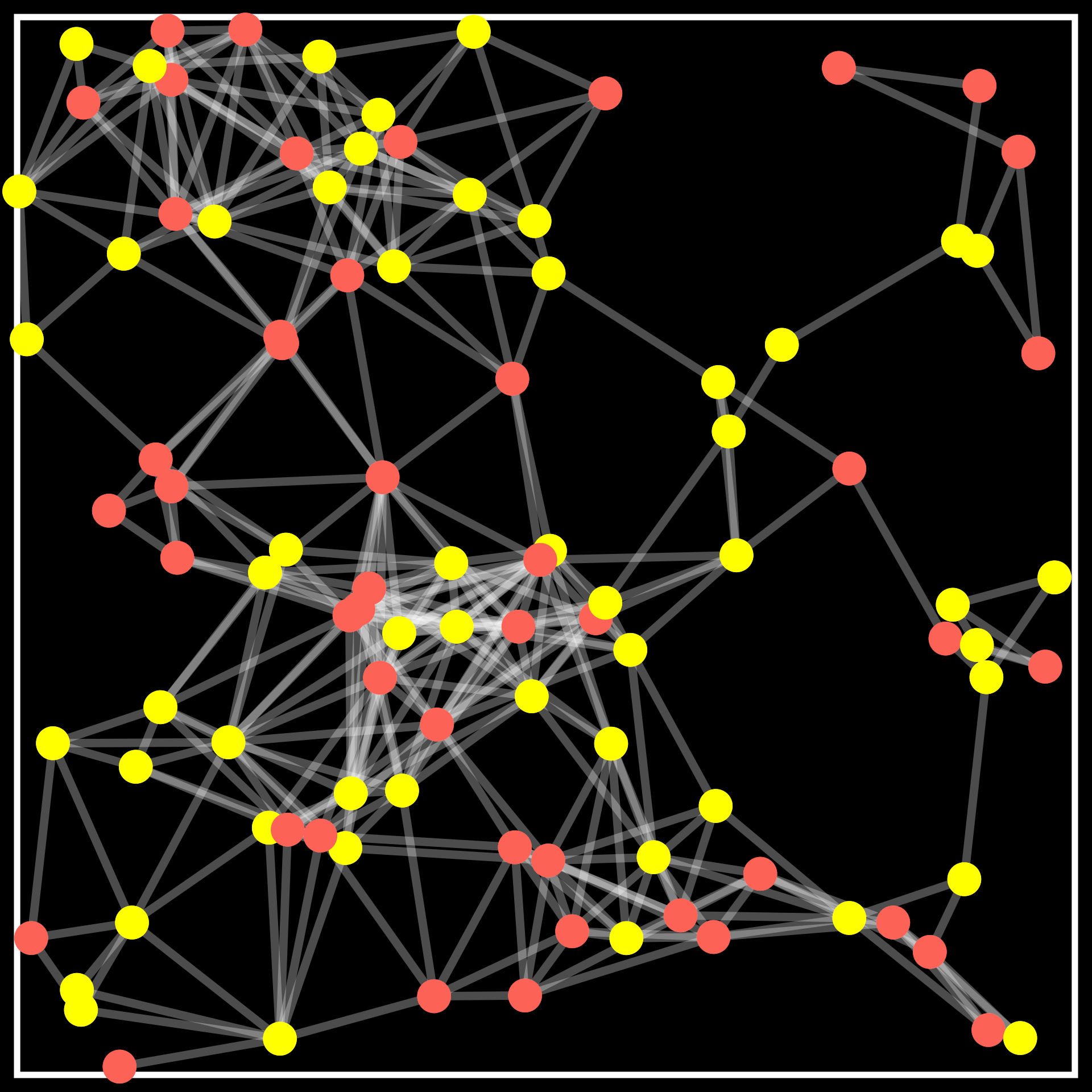
Problem Formulation
\(\mathbf{A}\) \(\sim GKBM(\lambda,n,d,\kappa_{\text{in}},\kappa_{\text{out}})\)
Problem: Given locations \(\mathbb{X}\), weights \(\mathbf{W}\), and graph \(\mathbf{A}\), recover \( \sigma_n\) exactly.

Prior work
- Abbe, E., Baccelli, F., and Sankararaman, A., 2021. Community detection on Euclidean random graphs. Information and Inference: A Journal of the IMA, 10(1), 109-160.
- Gaudio, J., Niu, X. and Wei, E., 2024. Exact community recovery in the geometric SBM. In Proceedings of the 2024 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), 2158-2184.
- Gaudio, J., Guan, C., Niu, X. and Wei, E., 2024. Exact Label Recovery in Euclidean Random Graphs. arXiv preprint arXiv:2407.11163.
Main results
Torus \( S=\left[\frac{-1}{2},\frac{1}{2}\right]^d\)

\(\mathbf{A}\) \(\sim GKBM(\lambda,n,d,\kappa_{\text{in}},\kappa_{\text{out}})\)
Achievability: If \(\lambda s >1\) and \(\lambda \mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}})> 1\), then there exists a linear time algorithm (in the number of edges) achieving exact recovery.
Impossibility: Idea
- Genie-based estimator: Given the communities of all nodes except the origin, find its community.
- Hypothesis testing problem: governed by the Chernoff-Hellinger divergence.
- Prob. of error \(\ge n^{-\lambda \mathbb{E}_W[I(w_0,W)]}\)
- Under some assumptions on the weight distribution, this can be strengthened to
Error probability \( \ge n^{-\lambda \mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}})} \) - Total number of errors \(\approx \lambda n^{1-\lambda \mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}})} \to \infty\) when \(\lambda \mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}}) < 1\)
Model-1d
Torus \( S=\left[\frac{-1}{2},\frac{1}{2}\right]\)


\(\mathbf{A}\) \(\sim GKBM(\lambda,n,p,q,\varphi)\)
- Poisson point process \(\mathbb{X}\)\(= \{X_u\}_{u=1}^N\) of intensity \(\lambda n\)
- Two communities: \( \sigma\)\( = \big(\sigma(1),\cdots,\sigma(N)\big)\) \[\mathbf{P}(\sigma(u)=\color{#f86d6d}{+1})=\mathbf{P}(\sigma(u)=\color{#ffde20}{-1}) = \frac{1}{2}\]
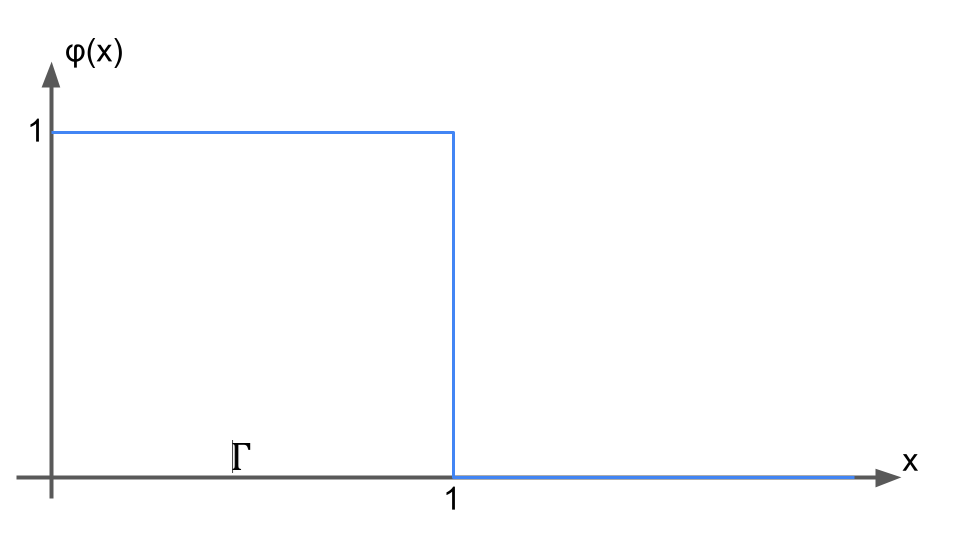
- Geometric kernel: \(\varphi: S \times S \to [0,1]\)
- Connection probabilities:
- Within community: $p$
- Between community: $q$
Given locations \(\mathbb{X}\) and communities \( \sigma\)
\[A_{uv}=1 \text{ w.p. }\begin{cases} p \varphi\Big(\|X_u-X_v\|\Big) & \text{if } \sigma(u)=\sigma(v)\\ q \varphi \Big(\|X_u-X_v\|\Big) & \text{if } \sigma(u) \neq \sigma(v) \end{cases}\]
Achievability
Q. How to recover the communities exactly when \(\lambda I_{\varphi}(p,q) > 1\)?Three phase algorithm:
Recall \(\color{#FF7F50}{\kappa}\): maximum interaction distance- Divide into blocks of size \(\frac{\color{#FF7F50}{\kappa}}{2}\frac{\log n}{n}\).
- Recover exactly in an initial block.
- Propagate from a recovered block to an adjacent block and so on.
- Number of mistakes in each block is at most a constant.
- Genie-based correction step
Initialization Phase
Propagation Phase
Refinement Phase
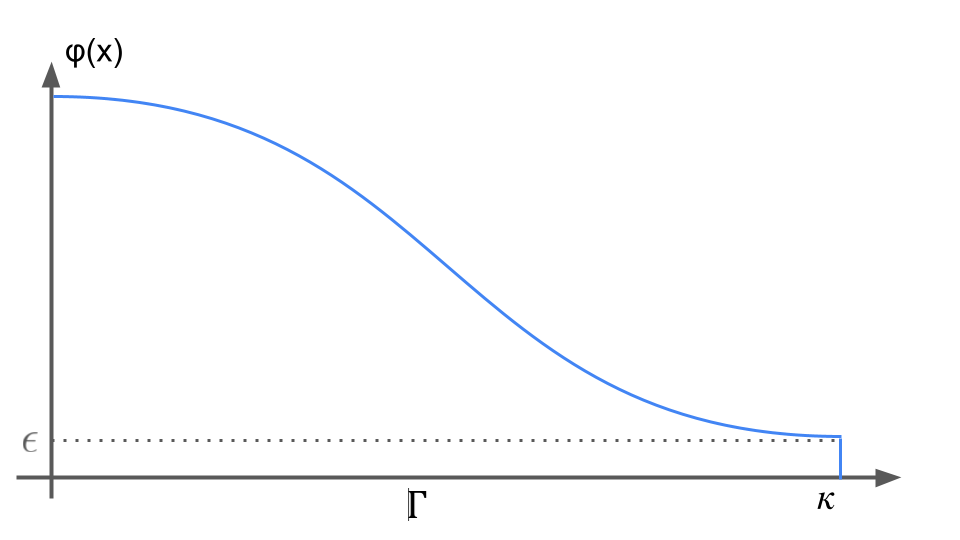
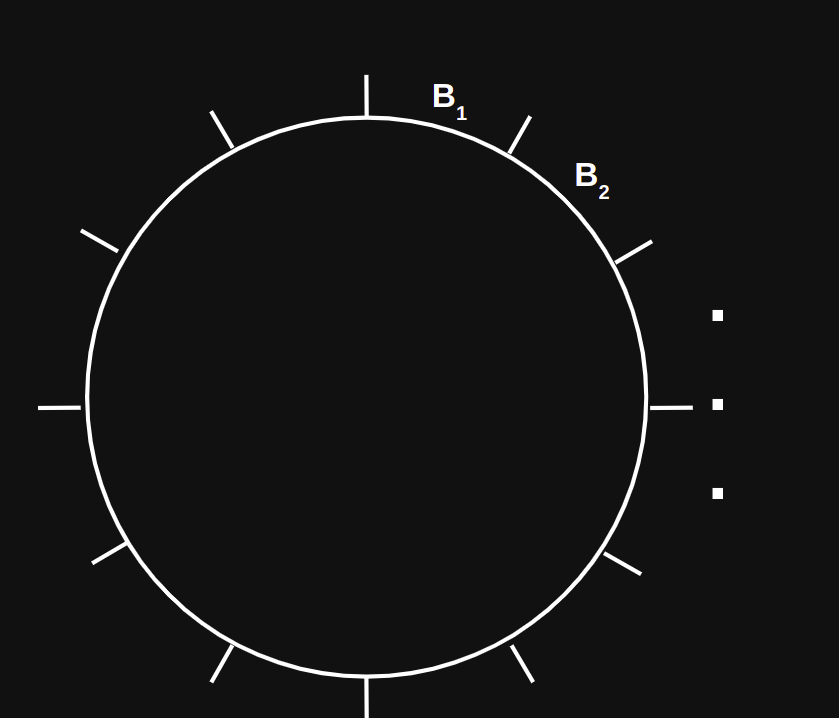
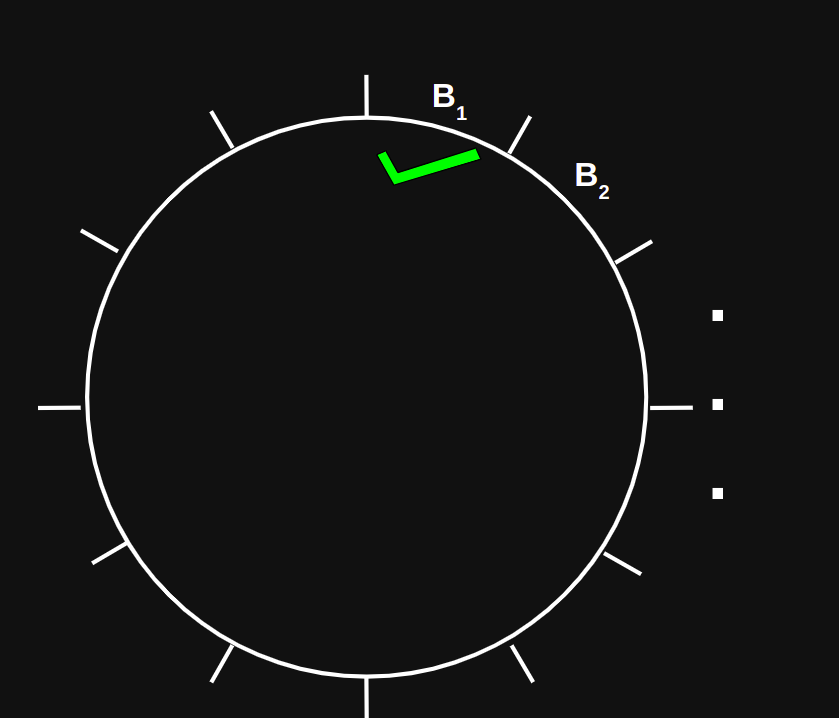
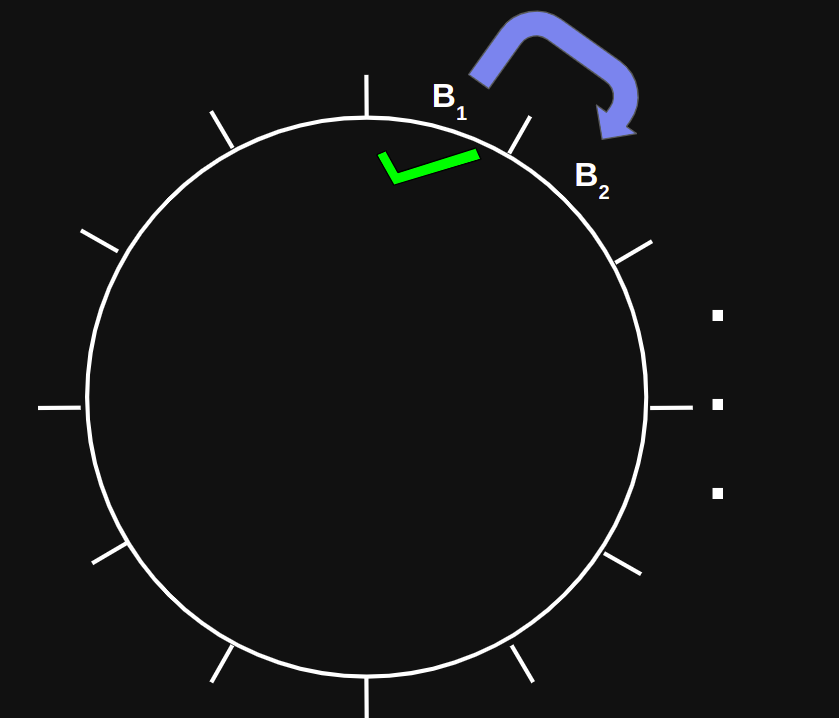
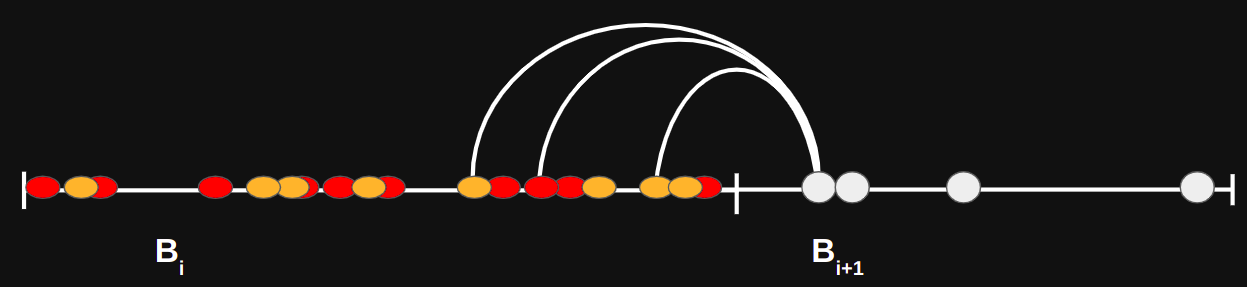
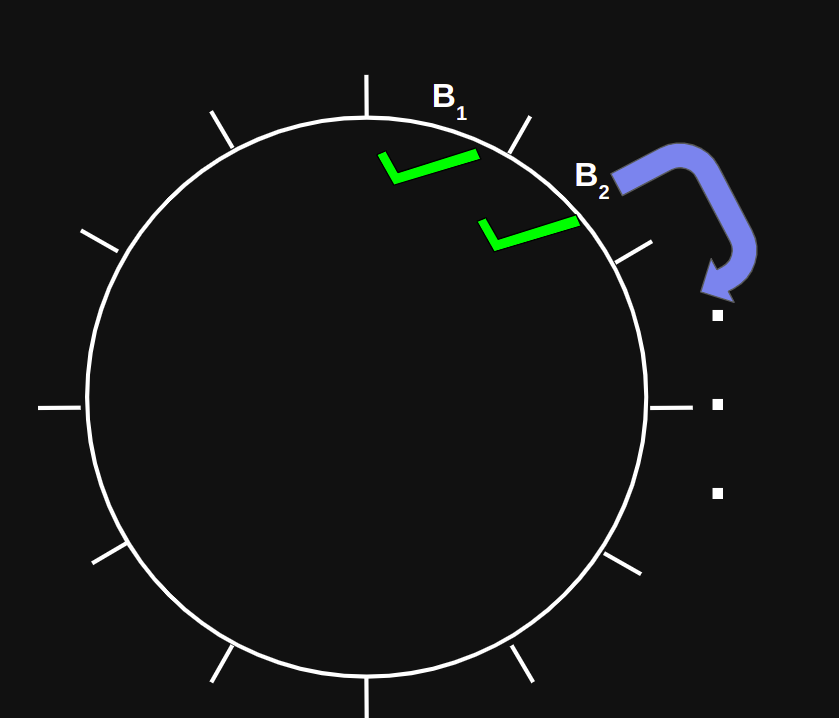
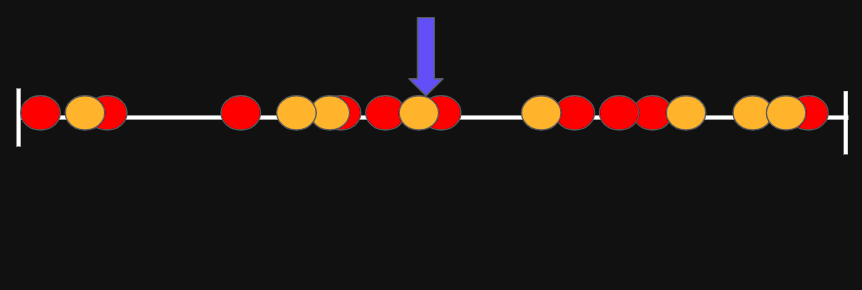
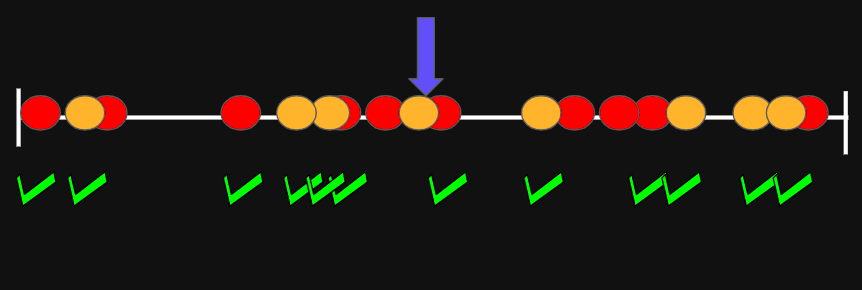
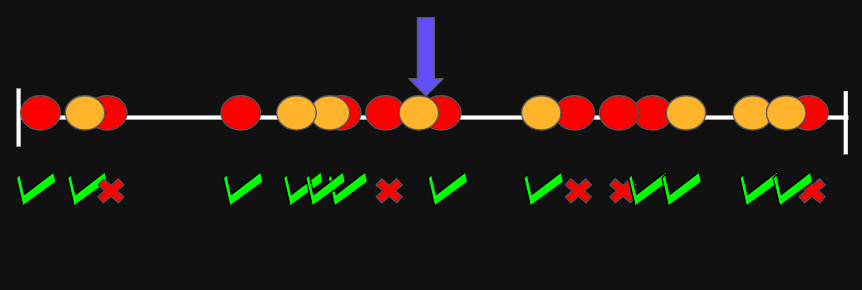
 Linear time algorithm
Linear time algorithm
Conclusions
- \(\lambda s<1\) or \(\lambda \mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}}) < 1\), then communities cannot be recovered.
- \(\lambda s>1\) and \(\mathcal{I}(\kappa_{\text{in}},\kappa_{\text{out}}) > 1\), then exact community recovery possible using a linear time algorithm.
- Multiple communities and higher dimensions.
- Main takeaway: Geometry helps in global inference tasks.
Future work
- Joint kernel estimation and community detection.
- Detecting communities with no information of location or in the semi-supervised regime.
- Spectral and SDP algorithms.
For community recovery
On networks with geometry;
Using the location,
Helps in detection,
In time that grows linearly.
Thank you !!